Kalorimetrischer Strömungssensor kann vielfältig individuell angepasst werden

11.07.2017 | Veröffentlicht in Ausgabe 07-2017

In einem interdisziplinären Projektteam hat Kriwan technische Innovation mit Ästhetik vereint. Entstanden ist ein Strömungssensor, der ein modulares Gehäusekonzept mit einer skalierbaren Hard- und Software kombiniert. Abgerundet wird dies durch ein spezielles Sensorelement, das selbst unter schwierigsten Bedingungen zuverlässig misst. Diethard Sawallisch und Thomas Roßmeißl, Forchtenberg

Die Luftstromgeschwindigkeit stellt eine wichtige Messgröße in lüftungstechnischen Anlagen dar und muss mittels für die jeweilige Anwendung geeigneten Sensoren erfasst werden. Dazu zählen die Identifikation der Verschmutzung bei Filtern, die Freischaltung der Heizung ab einer Mindestströmungsgeschwindigkeit bei Elektrolufterhitzern und auch die Regelung von Ventilatoren. Zur Erfassung der Luftstromgeschwindigkeit in HVAC & R-Systemen werden meist Differenzdrucksensoren oder kalorimetrische Strömungssensoren eingesetzt.

Breites Anforderungsprofil

Die Anforderungen aus den unterschiedlichen Anwendungen differieren oft untereinander. So wird beispielsweise für die Regelung von Ventilatoren oft ein sehr schneller Sensor benötigt, um zügig auf Störgrößen reagieren zu können. Für die Filterüberwachung hingegen genügt meist ein etwas trägeres System, da sich die Filter nur sehr langsam zusetzen. Jedoch muss bei der Filterüberwachung besonders hoher Wert auf die Verschmutzungssicherheit und gute Reinigungseigenschaften der Sensoren ge-legt werden.

Die physikalischen Gesetze der unterschiedlichen Messmethoden verhindern es jedoch oft, dass alle Anforderungen mit ein und demselben Sensor erfüllt werden können. So steht beispielsweise bei einem kalorimetrischen Strömungssensor die Anforderung eines sehr schnellen Sensors im Widerspruch zu der Anforderung eines mechanisch sehr stabilen und robusten Sensors. Die Reaktionszeit ist abhängig von der beheizten Masse. Je größer die Masse, desto träger ist der Sensor. Jedoch ist auch die mechanische Stabilität abhängig von der Masse. Je größer die Masse, desto stabiler ist der Sensor.

Diese und weitere Fakten gingen in die Auslegungskriterien eines neuen kalorimetrischen Strömungssensors von Kriwan (Bild 1) ein. Nachfolgend wird die Vorgehensweise während der Entwicklung ebenso geschildert wie die physikalischen Funktionskriterien des Sensors.

Messprinzip

Zwischen benachbarten Medien unterschiedlicher Temperatur findet so lange ein Wärmeaustausch statt, bis sich ein thermisches Gleichgewicht einstellt. Den Übertrag der Leistung nennt man Wärmestrom

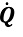
. Stellt man sich beispielsweise eine heiße Tasse Kaffee in einem Raum vor, so kühlt diese so lange ab, bis sich ein thermisches Gleichgewicht zwischen der Tasse und dem Raum eingestellt hat. Die Temperatur des Raumes ist dabei gestiegen. Die Messung der übertragenen Wärmemenge wird als Kalorimetrie bezeichnet.

Ein kalorimetrischer Strömungssensor nutzt folglich den Effekt des thermischen Gleichgewichtes, wobei ein Wärmestrom von einem Heizelement höherer Temperatur auf ein vorbeiströmendes Medium geringer Temperatur stattfindet. Das Medium mit der Masse m und der spezifischen Wärmekapazität c entzieht dem Heizelement durch Abkühlung um

die Energie

(0.1)

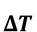
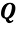
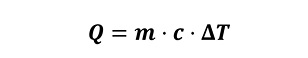
Die gleiche Energie muss vom Heizelement aufgebracht werden. Die Energie nach der Zeit abgeleitet, ergibt den Wärmestrom bzw. die Heizleistung

(0.2)

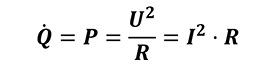
Um die aufgebrachte Wärmemenge des Sensors messtechnisch erfassen zu können, werden in der Praxis zwei unterschiedliche Verfahren eingesetzt, die Konstantstrom- (CCA) oder die Konstanttemperatur-Anemometrie (CTA). Dabei ist letzteres das meistgenutzte Verfahren, da es eine höhere Dynamik aufweist.

Das sogenannte Kingsche Gesetz be-schreibt die Wärmeübertragung von einem geheizten, langen zylindrischen Sensor in eine inkompressible Strömung ([1], S. 170). Dieses Gesetz ist eine theoretische Lösung der Nußelt-Zahl und bildet die Grundlage der Strömungsmessung.

Es gilt für den Wärmestrom:

(0.3)

mit der Temperatur des Heizelements

,der Temperatur des Mediums

, den von den physikalischen Randbedingungen abhängigen Konstanten A und B sowie der Strömungsgeschwindigkeit des Mediums

[2].

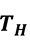
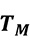
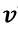
Für eine konstante Mediumstemperatur

sind

und R ebenfalls konstant, sodass sich Gleichung (0.3) wie folgt vereinfachen lässt (aus den Konstanten A und B werden die neuen Konstanten a und b).

(0.4)

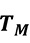
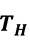
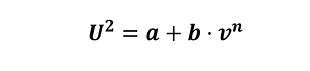
Die präzise Kalibrierung einer Strömungssonde liefert nun die Parameter a und b, wobei der Exponent n in guter Näherung 0,5 beträgt.

Heizleistung und Übertemperatur

Es muss nun zunächst die benötigte Heizleistung für den geforderten Messbereich bestimmt und im Schaltungskonzept entsprechend berücksichtigt werden. Das Erreichen der notwendigen Heizleistung wird im Wesentlichen durch die Widerstandskennlinie des Heizelements und durch die Höhe der Heizspannung beeinflusst.

Wie wird die Übertemperatur festgelegt?

Mithilfe einer Bilanzgleichung wird bestimmt, welche Leistung durch das vorbeiströmende Fluid entzogen wird. Hierbei muss insbesondere der gewünschte spätere Messbereich der Sonde berücksichtigt werden. Im Idealfall entspricht diese Leistung der vom Heizelement aufzubringenden Leistung; in der Realität wird zusätzliche Leistung aufgrund von Wärmeleitung (Erwärmung der benachbarten Struktur des Heizers) und Wärmestrahlung (in das Innere des Sensorkopfes) benötigt.

Die Bestimmung des Leistungsbedarfs erfolgt mit nachstehender Gleichung:

(0.5)

Fläche der Sonde längs der Strömungsrichtung

Übertemperatur (

-Heiztemperatur

-Mediumstemperatur)

Wärmeübergangszahl

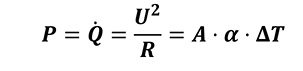
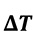
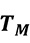
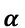
Die Übertemperatur bestimmt die Messauflösung der Strömungsgeschwindigkeit. Sie ist nach oben begrenzt durch die maximale Heizleistung des Heizelements und durch zunehmende Eigenkonvektion, nach unten durch eine zu geringe Messauflösung, welche in einem schlechten Signal-Rausch-Abstand (SNR) resultiert.

Temperaturkompensation

Das Medium, dessen Strömungsgeschwindigkeit

gemessen werden soll, hat innerhalb seines Aggregatzustands bestimmte von der Temperatur

abhängige stoffliche Eigenschaften, beispielsweise die Dichte, thermische Leitfähigkeit und Wärmekapazität, welche in der Wärmeübergangszahl

zusammengefasst werden.

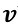
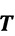
Eine rechnerische Bestimmung der Wärmeübergangszahl

nach ([1], S. 182) führt in etwa zu einem linearen Zusammenhang mit der Mediumstemperatur

(Bild 2).

Die Wärmeübergangszahl nimmt mit steigender Mediumstemperatur ab, der Wärmeübergang vom Heizer zum Medium wird also schlechter. Somit muss die Übertemperatur mit steigender Mediumstemperatur in dem Maße erhöht werden, dass gemäß Gleichung (0.5) eine konstante Heizleistung vorherrscht.

Wird die Heizleistung über der Mediumstemperatur nun konstant gehalten, ist sie nur noch abhängig von der Strömungsgeschwindigkeit

, welche sich in der Reynoldszahl verbirgt. Dies bedeutet, dass der Term

die Änderung der Wärmeübergangszahl

über der Mediumstemperatur kompensieren muss. Umgeschrieben folgt mit Gleichung 0.5 und der Reynolds-Zahl

(0.6)

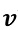
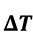
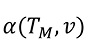
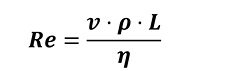
somit

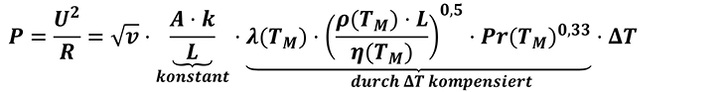
Die Heizleistung ist dann nur noch von der Quadratwurzel der Strömungsgeschwindigkeit abhängig (siehe auch [1], S. 183).

Erläuterung der Vorgehensweise bei der Mechanik des Sensorkopfes

Die Forderungen an den neuen Sensor sahen eine robuste, dichte und medienbeständige Ausführung vor, wobei der Sensor dennoch möglichst schnell sein sollte. Es sollte ein möglichst universell einsetzbarer und einfach montierbarer Sensor entstehen. Unter Anwendung der TRIZ-Methode konnte durch Lösung der physikalischen Widersprüche ein Konzept erarbeitet werden.

Vorüberlegungen

Je größer die Masse sowie die spezifische Wärmekapazität (siehe Formel 0.1) des Sensors bei gleichbleibender Temperaturdifferenz ist, desto mehr Energie steckt in dem System. Um dennoch eine hohe Reaktionsfähigkeit des Sensors erreichen zu können, das heißt die Wärme schnell aus dem System abzuführen, wird eine entsprechend große Oberfläche (siehe Formel 0.5) benötigt. Wird allerdings die Oberfläche bei gleichbleibender Geometrie und Abmaßen vergrößert, so wird die Verschmutzungsanfälligkeit erhöht und das Reinigungsvermögen verschlechtert.

Ein Beispiel hierbei ist der Kühler eines Autos. Eine filigrane Struktur und sehr dünnes Blech ermöglichen einen sehr guten Wärmeübergang. Auch die durch die Geometrie entstehenden Turbulenzen verbessern den Wärmeübergang, welche jedoch in der Strömungsmesstechnik für eine Verfälschung der Ergebnisse sorgen. Da eine Vergrößerung der Oberfläche auch fertigungstechnisch nur sehr aufwendig realisierbar ist und dadurch mit großen Kosten einhergeht, wurde versucht, über eine möglichst geringe Masse einen schnellen Sensor zu gestalten. Darunter leidet jedoch im ersten Moment die mechanische Festigkeit des Sensors (Bild 3).

Ziel war es also die Geometrie so zu entwerfen, dass trotz geringer Masse eine hohe mechanische Stabilität erreicht wird und die Materialien so ausgewählt werden, dass eine möglichst geringe Wärmekapazität vorliegt.

Konzepterstellung

Eine kugelförmige Geometrie weist trotz sehr dünner Wandstärken eine hohe mechanische Festigkeit auf. Weiterhin kann bei einer kugelförmigen Geometrie durch Rotationssymmetrie eine Richtungsunabhängigkeit erreicht werden. Fertigungstoleranzen können durch die Selbstzentrierung des Heizelementes an dem Kugelsegment beim Anbringen im Fertigungsprozess auf ein Minimum reduziert werden. Dagegen spricht allerdings, dass eine Kugel von allen Körpern die kleinste Oberfläche bei vorgegebenem Volumen hat.

(0.8)

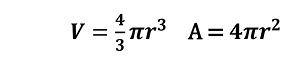
Da die Vorteile der Kugelgeometrie jedoch überwiegen, wurde diese für die weiteren Schritte als Grundlage verwendet.

Durch den folgenden Aufbau (Bild 4) konnte bei geringer Masse ein robuster, richtungsunabhängiger, verschmutzungssicherer und schneller Sensor entstehen.

Im Kugelsegment befindet sich der Heizer. Dieser wird thermisch vom im Ring befindlichen Temperatursensor durch einen Kunststoff entkoppelt. Der Temperatursensor wird wiederum thermisch vom Befestigungsrohr entkoppelt.

In der nachfolgenden Simulation (Bild 5 und Bild 6) wurden unterschiedliche Varianten der Geometrie untersucht, um ein Optimum aus thermischer Entkopplung und mechanischer Festigkeit (Wandstärke und Länge) zu erreichen.

Variiert wurden bei den unterschiedlichen Varianten die Wandstärke sowie der Abstand zwischen Heizer und Temperatursensor. Eine Verringerung der Wandstärke sowie Vergrößerung des Abstands ermöglichen eine bessere thermische Entkopplung zwischen den Sensorelementen. Da es durch Eigenthermik bedingt in der Realität niemals eine Nullströmung gibt, wurden die Varianten exemplarisch auch anhand von 0,1 m/s Strömung simuliert. Die Variante 3 wurde anschließend als Grundlage für den Bau weiterer Prototypen verwendet, anhand derer die Simulationsergebnisse in der Praxis wiederholt wurden (Bild 7).

Mit diesen Prototypen konnten die Simulationsergebnisse bestätigt werden (Bild 8). Sie wurden als Basis für den Bau eines Spritzgusswerkzeuges verwendet.

Entwurf einer Messeinrichtung

Die Messung der Mediumstemperatur wie auch die Regelung der Übertemperatur werden von einem Mikroprozessor übernommen. Hierdurch ist es nicht nötig, eine Wheatstonesche-Messbrücke einzusetzen. Besser ist die Temperaturmessung in einem separaten Zweig mit konstanter Spannung, da dort dann nur der Widerstandswert temperaturabhängig variiert.

Die Heizspannung U_B sollte sehr präzise sein, da es als Messreferenz für die Analog-Digital-Wandler (ADC) verwendet wird.

Das Schaltungskonzept (Bild 9) bietet den großen Vorteil der Flexibilität hinsichtlich der Wahl des Sensor- und Heizelementes gegenüber herkömmlichen Messbrücken mit Operationsverstärkern, bei welchen lediglich das Differenzsignal der Messzweige ausgewertet wird. Beispielsweise wäre eine genaue Temperaturkompensation, wie in Kapitel Temperaturkompensation gezeigt, damit nicht möglich.

Regelung

Geregelt wird die Übertemperatur des Heizelements. Die Stellgröße hierfür ist die Heizspannung U_H, die per Pulsweitenmodulation (PWM) variiert wird. Für die Regelung der Übertemperatur ist eine ausreichende Heizleistung erforderlich, um in allen Situationen die nötige Übertemperatur mit ausreichender Dynamik zu erreichen.

Anhand der ermittelten Sprungantwort des Prototyps des Sensorkopfs wurde die Regelstrecke mit einem PT1-Verhalten identifiziert. Dies bedeutet, dass der verwendete Regler einen I-Anteil besitzen muss, um stationär genau, d. h. ohne bleibende Regeldifferenz, regeln zu können. Beschleunigen lässt sich das reine I-Verhalten durch einen Proportional-Anteil. Daher wird ein PI-Regler gewählt. Der vereinfachte Regelkreis ist Bild 10 zu entnehmen.

Da der Regler mittels Mikroprozessor realisiert werden soll, muss die Reglergleichung aus einem zeitkontinuierlichen Regler diskretisiert werden. Mithilfe der z-Transformation und weiterer Umformungen erhält man die gängige Form:

(0.9)

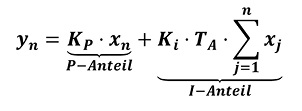
Diese vereinfachte Gleichung ist nun klar in P- und I-Anteil aufgeteilt und lässt sich als Regelalgorithmus in C-Code abbilden.

Ergebnisse der Kalibrierung

Mit dem Kingschen Gesetz ergibt bei n = 0,5 die Funktion

eine Gerade. Dies ist in Bild 11 zu erkennen. Die Messpunkte mit dem Sensor sind blau dargestellt, woraus die Ausgleichsgerade (violett) berechnet wird. Hieraus lassen sich die Steigung (b) und der Offset (a) ermitteln.

Die beiden Parameter werden nun be-nötigt, um aus der Heizspannung die Strömungsgeschwindigkeit zu bestimmen. Hierzu wird das Kingsche Gesetz nach

umgestellt.

(0.10)

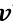
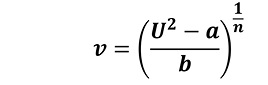
Wie erwartet, zeigt sich im direkten Zusammenhang eine sehr gute Übereinstimmung des Sensors mit dem Kingschen Gesetz (Bild 12).

Geringe Drehrichtungsabhängigkeit

Mit dem erstellten Prototyp konnte die Annahme der geringen Richtungsabhängigkeit aus der Konzepterstellung bestätigt werden (Bild 13). Bei 0,5 m/s beträgt die Abweichung rund 1 Prozent vom Mittelwert.

www.kriwan.de