Dabei ist es wichtig, eine möglichst hohe Stückzahl in möglichst kurzer Zeit zu erreichen. Dazu bietet die Kältetechnik ein breites Spektrum an Möglichkeiten, denn das Abkühlen des Werkstücks in der Form ist ein maßgeblicher Faktor für die Geschwindigkeit der Produktion. Das Prinzip einer Spritzgießmaschine stellt Bild 1 dar.
Die Auslegung einer Kühlanlage für diesen Einsatzzweck ist schwierig, weil sich die Arbeitsbedingungen in der Spritzgussteilfertigung häufig ändern: Die Materialien ändern sich von Bauteil zu Bauteil, ebenso die Geometrie und Masse des Werkstücks. Eine punktgenaue Leistungsauslegung ist in der Praxis daher nicht möglich. Um die maßgeblichen Auslegungskriterien dennoch in den Griff zu bekommen, ist eine gründliche Vorab-Planung sinnvoll.
Dazu werden empirisch ermittelte Größen eingeführt, die sich aus der Erfahrung mit einer Vielzahl von ähnlichen gebauten Anlagen für den vorgegebenen Einsatzzweck ergeben haben.
Anhand eines Beispiels eines häufig vorkommenden Anwendungsfalls in einer Produktionsstätte wird im Folgenden eine Auslegungsberechnung mittels grundlegender Gleichungen erläutert. Dies erlaubt ein näheres Verständnis des technisch/physikalischen Prozesses.
Verfahren des Spritzgießens und die benötigte Kältetechnik
Das Verfahren besteht darin, dass geeigneter Kunststoff als Granulat durch Beheizung auf 250 bis 300 °C innerhalb der sog. Spritzeinheit aufgeschmolzen und in eine Form gepresst wird. Die Form besteht aus zwei Hälften, die mithilfe eines hydraulischen Antriebs zusammen- und wieder auseinandergefahren werden. Im zusammen gefahrenen Zustand wird der Kunststoff eingespritzt. Der Kunststoff kühlt auf eine niedrige Entnahmetemperatur aus, wird hart, die Form fährt auseinander und die fertigen Bauteile werden ausgestoßen. Die Form nennt man auch Werkzeug.
Die Aushärtung geschieht durch Entzug von Wärme. Das Material wurde auf ein Temperaturniveau von 250–300 °C aufgewärmt und aufgeschmolzen, wird dann auf eine Temperatur von ca. 40 °C in der Form heruntergekühlt und nimmt einen festen Aggregatzustand ein. Je schneller der Wärmeentzug und damit die Temperaturabsenkung erfolgt, desto höher ist folglich auch die Produktionsgeschwindigkeit, der maßgebliche Faktor für eine rentable Teileproduktion.
Die Kühlwirkung erreicht man vornehmlich mit Kaltwasser, welches durch zahlreiche Bohrungen/Kanäle mit hoher Fließgeschwindigkeit durch die Form geführt wird. Über die Oberflächen der Bohrungen wird die Wärme aus dem Werkstück an das Kaltwasser übertragen. So ist diese Form als Wärmeübertrager zu betrachten.
Prinzipiell wird eine Kühlleistung Q·0 verlangt, die für eine Produktionsmenge pro Zeiteinheit (kg / h) an Wärme in das Material zuvor eingegeben wurde.
Durch die Erhitzung zur Verflüssigung des Rohmaterials erhöht sich dessen Wärmeinhalt, den wir als Enthalpie in Kilojoule pro Kilogramm (kJ / kg) bezeichnen. Eine Berechnung dieser Wärmemenge vergleichbar mit dem Erwärmungs-/ Abkühlungsvorgang bei anderen Materialien, wie zum Beispiel Wasser (fest, flüssig, gasförmig), kann nicht angewendet werden. Kunststoffe haben keine festen Schmelzpunkte und auch keine festen Erstarrungspunkte. Auch ist die spezifische Wärmekapazität über den Temperaturverlauf nicht konstant. Es gibt im Erwärmungs-/Abkühlvorgang verschiedene Temperaturpunkte, in denen das molekulare Gefüge verändert wird.
Der Kältebedarf / Kälteleistung und Maschinenauswahl
Daher bedient man sich zur Feststellung des erforderlichen Kältebedarfs der Enthalpie. Diese wird definiert als ein Wärmeinhalt auf einem bestimmten Temperaturniveau. So gibt es einen spezifischen Enthalpiewert bei der Temperatur zu Beginn und einen am Ende des Abkühlprozesses bei der entsprechenden Temperatur. Die Werte für die spezifische Enthalpie h in kJ/kg kann man Tabellen und Grafiken entnehmen, s. z. B Bild 2.
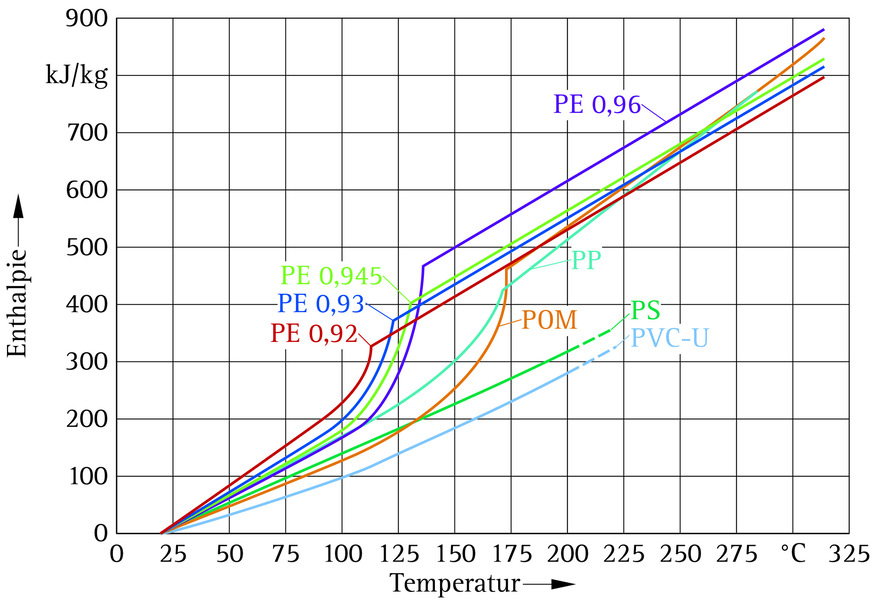
Bild: VDMA
Beispiel
In einer Fertigung mit 10 Spritzgießmaschinen werden insgesamt in einer Stunde 500 kg/h Kunststoff aus PE 92 verarbeitet. Diese verarbeitete Menge in einer
Zeiteinheit (hier 1 Stunde) bezeichnet man als Kunststoff-Massendurchsatz/Stunde m·ku in kg/h.
Die Temperatur der Schmelze betrage 240 °C, die Endtemperatur nach Kühlung (Entnahmetemperatur des Produkts) betrage 40 °C.
Die spezifische Enthalpie beträgt in diesen Temperaturpunkten gemäß Abbildung 2 h240 = 620 kJ/kg bzw. h40 = 40 kJ/kg.
Der abzuführende Wärmestrom ist damit
Q·0m = m·k ∙ (h240 – h40 )
= 500 kg/h ∙ (620 – 40) kJ ⁄
(kg = 290 000 kJ / h)
= (290 000 kJ / h) / ((3,6 ∙ 1000 Wh / kJ))
= 80,5 kW
bzw. 80,5 kW/500 kg = 0,161 kWh pro kg
Zu diesem Kältebedarf (allein zur Verfestigung der Kunststoff-Masse) sind erhebliche Verlustleistungen zu addieren.
Diese sind:
der Kaltwasserpumpen
Diese Werte könnte man mit einiger Mühe berechnen. Da sie aber je nach Produkt sehr unterschiedlich sind, kann sinnvoller Weise in erster Näherung ein empirischer Faktor a in kWh/kg aus der Erfahrung einer Vielzahl ausgewerteter Anlagen eingeführt werden.
Dabei ist zu bewerten, ob es sich um eine schnelllaufende Produktion von z. B. Verpackungsartikeln oder von technischen Präzisionsteilen handelt.
Mit a = 0,25 kWh/kg (mittlere Wärmemenge) kommt man der endgültigen Berechnung z. B. im Verpackungsbereich sehr nahe. Damit ist der einzusetzende Kältebedarf in erster Näherung:
Q·0 = m·Ku ∙ a in [kg / h ∙ kWh / kg] = kW
Das entspricht einem deutlich höheren Wert gegenüber dem grundsätzlichen Kältebedarf für die Verfestigung des Kunststoff-Produkts.
Die Kälteleistung der Kältemaschine ist damit bestimmt zu:
Q·0 = 500 kg⁄h ∙ (0,25 kWh / kg) = 125 kW.
Diese Leistung sollte im praktischen Einsatz zur Verfügung stehen, um einen gesicherten Betrieb bei unterschiedlichen Kunststoffen und Produktionsgeschwindigkeiten zu gewährleisten. Zusätzlich sind die Heißkanäle zu berücksichtigen.
Die Strömung des Kaltwassers / Wärmeübertragung
Diese Kühlleistung muss über die Oberflächen der eingebauten Kühlkanäle auf die Formen der vorhandenen SGM und der Kunststoffmasse übertragen werden. Dies ist – wie in allen Wärmeübertragern – ein Vorgang der allgemeinen Wärmedurchgangs-Gesetze: der Wärmeleitung und der Wärmeübertragung (Konvektion).
a) Wärmeleitung
Die Wärme strömt vom heißen Kunststoff mit t=240 durch das Werkzeugmaterial (legierter Stahl) zum Kaltwasser.
Für den Wärmedurchgang Q·L gilt:
Q·L = λ / δ ∙ A ∙ (t2 – t1 )
Dabei sind:
Q·L = Wärmestrom in W
λ = Wärmeleitkoeffizient in W/(m∙K)
δ = Schichtdicke in m
A = Wandoberfläche in m2
t2 = Oberflächentemperatur auf Seiten des Kunststoffs in °C
t1 = Oberflächentemperatur außen auf der Kaltwasserseite in °C
Die Gleichung des Wärmedurchgangs sagt aus:
Daraus ergeben sich für die Konstruktion des Werkzeugs folgende sinnvolle Maßnahmen:
In modernen Werkzeugen werden die Kühlbohrungen sehr weit nach außen in die Nähe des Kunststoffs, also in die Nähe des Produkts gelegt. (Man nennt dies auch konturnahe Kühlung.)
Auf der Kunststoffseite lässt sich der Wärmeübergang nicht beeinflussen, wohl aber auf der Kaltwasserseite. Durch einen hohen Kaltwasserstrom ergibt sich eine sehr geringe Temperaturdifferenz zwischen Ein- und Austritt des Kaltwassers und damit auch eine gleichmäßige Temperierung der Fläche.
b) Wärmeübergang (Konvektion)
Der Wärmeübergang, auch Konvektion genannt, ist eine Wärmeübertragung von einem festen Material auf ein Fluid bzw. umgekehrt. Auch hier ist die Intensität des Wärmeübergangs auf der Produktseite nicht zu beeinflussen. Wohl aber ist eine enorme Beeinflussung auf der Kaltwasserseite möglich. Aufgrund unterschiedlicher Fluide auf beiden Seiten der Formwandung unterscheiden sich auch die Größen der Wärmeübergangskoeffizienten und der jeweiligen Temperaturen. Diese Vorgänge können durch folgende Grundgleichungen beschrieben werden:
Q·W1= α1 ∙ A ∙ (tO1 – tF1)
Q·W2= α2 ∙ A ∙ (tO2 – tF2)
Dabei sind:
Q·W = Wärmestrom in W
α = Wärmeübergangskoeffizient
in W/(m2∙K)
A = Wandoberfläche in m2
tO = Oberflächentemperatur auf der Produktseite (Temperatur des Kunststoffs) bzw. auf der Kaltwasserseite in °C
tF = Temperatur des Kunststoffs bzw. des Kaltwassers in °C
Der Gesamtwärmestrom ergibt sich aus der Summe aus Wärmeleitung und Wärmeübergang zu
Q·o = Q·L + Q·W1 + Q·W2.
Der Wärmeübergang bestimmt sich auf der Kaltwasserseite durch die Intensität der Strömung. Eine starke Strömung ist turbulent. Es bilden sich keine Strömungsschichten, wie bei der sog. laminaren Strömung, da innerhalb des Rohrs in der Strömung zusätzliche Störbewegungen den Wandkontakt intensivieren. Diese turbulente Strömung muss erreicht werden, um einen optimalen Wärmeübergang zu erzielen. Eine Berechnung ist sehr komplex und nur mit umfangreichen Gleichungen und Kennzahlen näherungsweise durchzuführen.
Mittels der Reynoldszahl ist eine Aussage möglich, ob eine Strömung turbulent ist. Sie stellt den Zusammenhang zwischen der Strömungsgeschwindigkeit, dem Rohrdurchmesser und der kinematischen Viskosität des Mediums (Kaltwasser) dar:
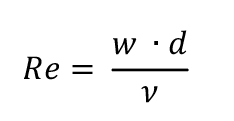

Dabei sind:
Re = Reynoldszahl
w = Strömungsgeschwindigkeit in m/s
d = Rohrdurchmesser in m
ν = kinematische Viskosität in m²/s
Eine Strömung ist turbulent, wenn Re > 2000 ist, max. 10000.
Eine hohe Strömungsgeschwindigkeit vergrößert die Reynoldszahl. Eine hohe Reynoldszahl bedeutet starke Turbulenz und damit einen großen Wärmeübergangskoeffizienten bzw. hohen Wärmeübergang. Die Gleichung zeigt aber auch, dass sich z. B. der Zusatz von Wasserzusatzmitteln wie Glycol/Frostschutz durch Vergrößerung der Viskosität dem besseren Wärmeübergang nicht zuträglich ist.
Eine Verbesserung der Turbulenz kann auch erreicht werden durch Einbauten in den Kühlkanälen sowie durch Reibung an aufgerauten Oberflächen.
Eine große Strömungsgeschwindigkeit bedingt einen sehr starken Kaltwasserstrom, was zwangsläufig dazu führt, dass die Temperaturdifferenz zwischen dem Kaltwasserstrom-Eintritt und -Austritt ∆tW sehr klein ist, etwa 2 K. (Zum Vergleich: In der Klimatechnik beträgt diese Differenz üblicherweise 5 bis 6 K.)
Ein hoher Druckverlust in der Kaltwasserleitung und im Werkzeug mit dem damit verbundenen höheren Energieaufwand muss dafür in Kauf genommen werden.
Dimensionierung von Kaltwasser-Strom und Rohrleitung
Der Kaltwasserstrom berechnet sich nach:
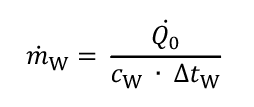

Dabei sind:
∆tW = Temperaturdifferenz Wasseraustritt – Wassereintritt in K
Q·o = Kältebedarf/Kälteleistung in kW
cW = spezifische Wärmekapazität, für Wasser z. B. 4,19 kJ/(kg K)
Zur Förderung des Kaltwassers ist daher eine hohe Druckenergie erforderlich. Üblicherweise beträgt der Differenzdruck 3 bar, sodass die gewünschte turbulente Strömung erreicht wird. Zusätzlich müssen noch die Strömungsverluste auf der Rücklaufseite überwunden werden.
Erfahrungsgemäß kann der Druckverlust durch die Strömung in den Leitungen mit 1 bar angenommen werden (ausgehend von einer Strömungsgeschwindigkeit im Rohr von 2 m/s). Soll der Druckverlust auf Rücklaufseite 1 bar betragen, so muss die Kaltwasserpumpe einen in Summe einen Druck von 5 bar liefern. (Überwindung von Druckverlusten 1 bar auf Vorlauf, 1 bar auf Rücklaufleitung, 3 bar über das Werkzeug)
Die Durchmesser der Rohrleitungen werden in erster Näherung durch die Durchflussgleichung bestimmt. Diese stellt den Zusammenhang zwischen dem Volumenstrom V·W in m3/s und der Strömungsgeschwindigkeit w in m/s des Wassers her:
 bzw. 
Der Volumenstrom des Wassers ergibt sich aus dem spezifischen Gewicht ρ= 1000 kg/m3 zu:
V·W = m·W / ρ
Beispiel
Bei einem Kältebedarf von z. B. 125 kW und der erforderlichen Temperaturdifferenz von 2 K ergibt sich ein Volumenstrom V·W:


Mit der in der Praxis üblichen Strömungsgeschwindigkeit von 2 m/s ergibt sich die erforderliche Querschnittsfläche der Rohre A:
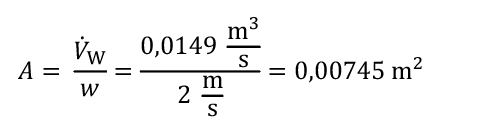

Aus der Kreisgleichung A= π ∙r 2 folgt für r:
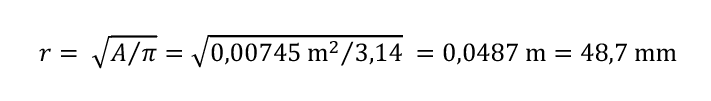

bzw. den Rohrinnendurchmesser von
d = 2 ∙ r = 97,4 mm
Der Druckverlust auf der Leitung ist hier nicht berücksichtigt, sodass davon auszugehen ist, dass die Hauptleitung z. B. ein Kunststoffrohr DN100 sein sollte, mit der Druckfestigkeit 16 bar.
Die Rücklaufleitung wird genauso gestaltet.
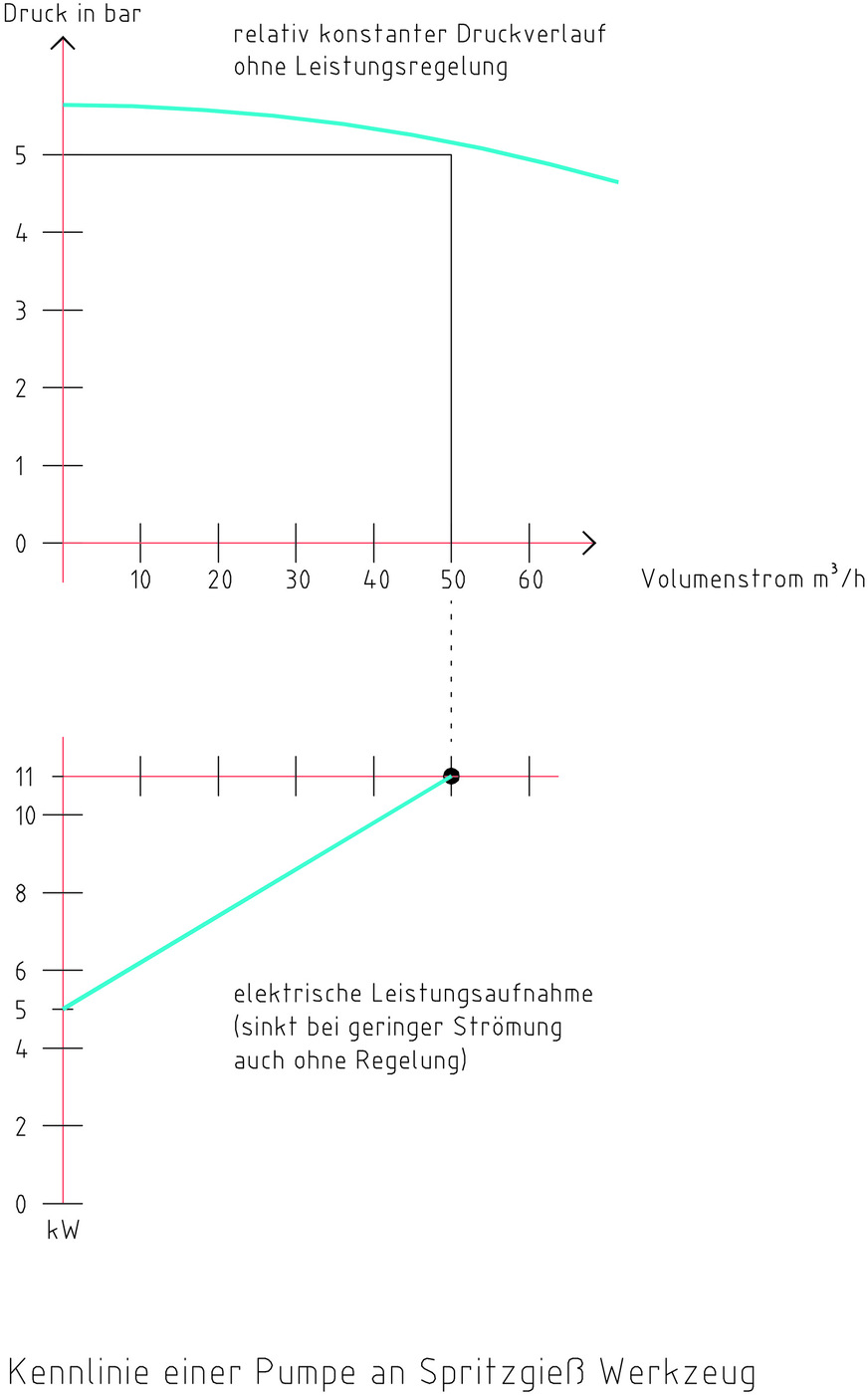
Bild: Reisner + Kettler GmbH
Kaltwasser-Anlage
Vorwiegend werden diese Anlagen in einem sog. atmosphärisch offenen System gebaut, nicht wie in der Klimatechnik im geschlossenen System Dabei wird ein Tank aufgestellt, an dem die Pumpenanlage angeschlossen wird. Das rücklaufende Wasser hat nur den Staudruck der Rücklaufleitung zu überwinden. Das garantiert die erforderliche Druckdifferenz zwischen Vorlauf am Werkzeug und Austritt, die wichtig ist für die intensive, sprich turbulente Strömung.
Zweckmäßigerweise wird dieser Tank als eine hydraulische Weiche gestaltet, mit zwei Temperaturzonen für Vorlauf und Rücklauf. An der Rücklaufzone (warme Seite) werden entsprechend der Anzahl an Kältemaschinenverdampfern die Zirkulationspumpen für die Kältemaschinen eingesetzt, die dadurch autark mit konstanter Strömung die Verdampfer versorgen, auf der kalten Seite werden die Versorgungspumpen für die Werkzeuge angeschlossen.
Die Kältemaschinen-Verdampfer müssen sich für so hohe Kaltwasserdurchsätze eignen. Bündelrohrverdampfer mit einer Rohrbündel-Wandstärke von üblicher Weise 0,2 bis 0,3 mm sind aus Sicht des Verfassers sicher ungeeignet genauso wie Plattenverdampfer.
Die Pumpenanlage
Die Pumpe wird ausgelegt auf den Kaltwasservolumenstrom sowie die zu überwindende Druckdifferenz, im obigen Beispiel für gerundet 54 m3/h.
Dies entspricht in diesem Beispiel der Pumpenkennlinie in Bild 3:
Zu beachten ist, dass die Strömungs-Belastung der Pumpe je nach Auslastung der Produktion unterschiedlich ist, der Druck aber immer gleich hoch am Werkzeug stehen muss – unabhängig von der Auslastung der Produktion, denn sonst ist die erforderliche Strömung im Werkzeug nicht gewährleistet. Also muss der hohe Druck gewährleistet sein, unabhängig davon, ob nur eine Form in Betrieb ist oder alle.
Die Leistungsaufnahme passt sich aufgrund der physikalischen Gegebenheiten von selbst an, weil der Antriebsmotor annähernd nur die elektrische Leistung aufnimmt, die einem Förderstrom entspricht.
Eine heute übliche belastungsabhängige Drehzahl-Regelung der Pumpe ist damit nicht sinnvoll anzuwenden. Die volle Drehzahl der Pumpe ist für die Aufrechterhaltung des Wasserdrucks notwendig. Eine Verfolgung der Pumpenkennlinie zeigt, dass die elektrische. Leistungsaufnahme ohne Regelung von dem Förderstrom abhängig ist und auch ohne Regelung proportional dazu sinkt.
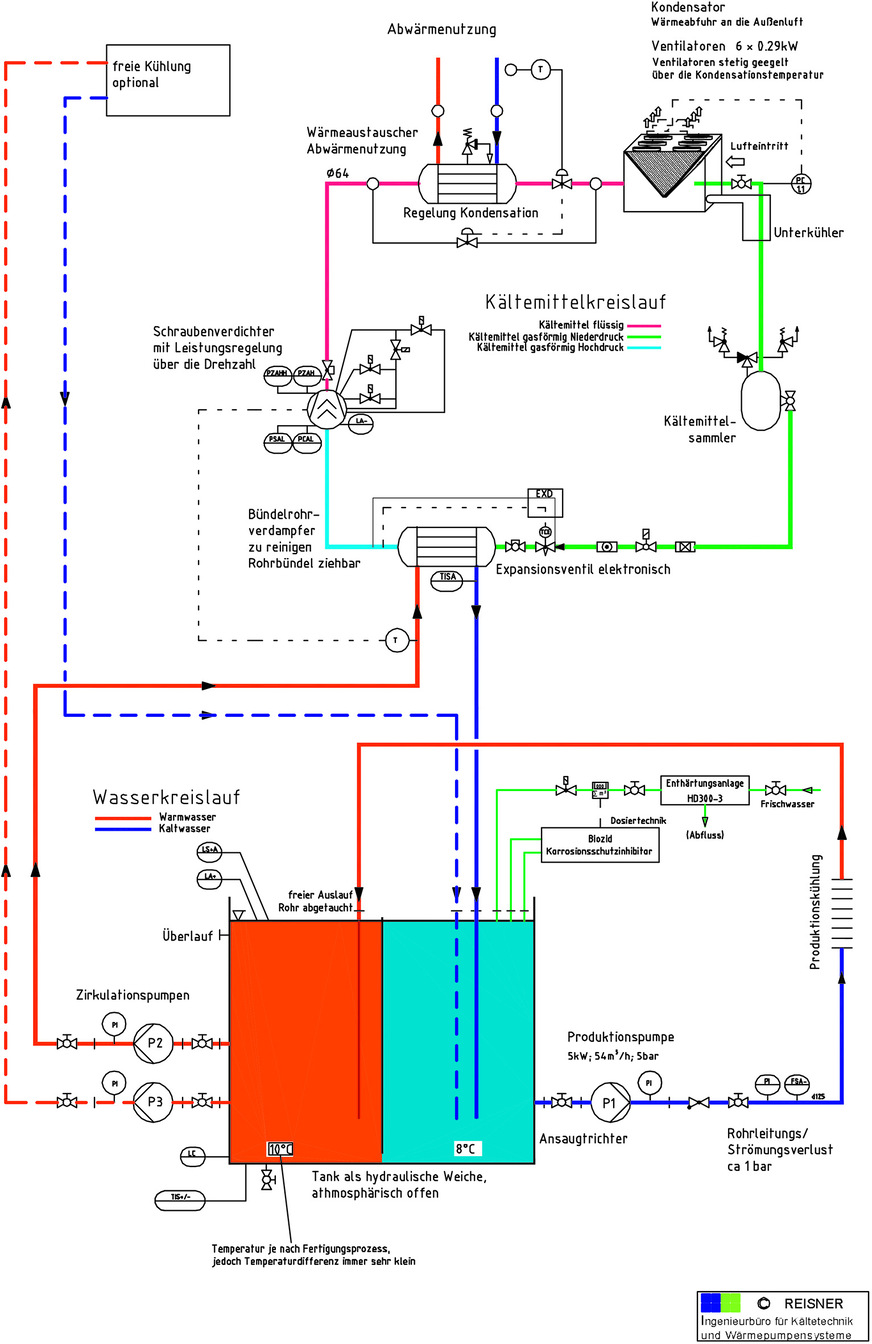
Bild: Reisner + Kettler GmbH








